摘 要:针对教学过程中永磁同步电机(permanent magnet synchronous motor, PMSM)直接转矩控制(direct torque control, DTC)理论不易理解,建模困难等问题,详细介绍了PMSM DTC系统各个环节的MATLAB/Simulink建模方法。基于PMSM在αβ坐标系下的数学模型,将采样到的三相定子电流、电压通过坐标变换送入磁链、转矩估算模型,结合电机转子位置,磁链和转矩误差信号合理选择逆变器的开关矢量,以达到电机调速的目的。在改变转速和突加负载的情况下对系统进行仿真,结果表明,该系统具有很好的转速、磁链、转矩响应,从而验证了该模型的有效性,同时也为PMSM DTC的软硬件设计提供了理论基础。
关键字: PMSM;DTC;仿真
Abstract: In order to deal with these problems about permanent magnet synchronous motor (PMSM) direct torque control (DTC) theory in the teaching process, which is difficult to understand, modeling difficulties and other issues, all aspects of the DTC system MATLAB / Simulink modeling method is introduced in detail. based on the mathematical model in the αβ coordinate system, sampling to the three-phase stator current and voltage are admitted the flux and torque estimation model through the coordinate transformation, it is a reasonable choice of the inverter switching vector, combined with the rotor position, flux and the torque error signal, to achieve the purpose of the motor speed. The simulation is carried out in the case of changing the speed and suddenly increasing in load, the results show that the DTC system gives a good response to the rotation, flux and torque, which show that the model is effective, and the method provides a base for software and hardware design of an actual PMSM DTC.
Key words: PMSM; DTC; Simulation
引言
随着电力电子技术、微型计算机技术、稀土永磁材料和控制理论的飞速发展,PMSM具有体积小、重量轻、效率高、转动惯量小、可靠性高等优点已获得越来越广泛的应用,将DTC策略应用于PMSM控制中,以提高电机的快速转矩响应,成为研究者关注的课题。
直接转矩控制理论于20世纪80年代由德国学者M.Depenbrock和日本学者I.Takahashi首先针对异步电动机提出,90年代由Zhong.L,RahmanMF,Hu.YW等学者提出PMSMDTC理论[6]。其基本思想是将电机给定转速和实际转速的误差,经PI调节器输出作为转矩的给定信号;同时系统根据检测的电机三相电流和电压值,利用磁链模型和转矩模型分别计算电机的磁链和转矩的大小,计算电机转子的位置、电机给定磁链和转矩磁链与实际值的误差;最后根据它们的状态选择逆变器的开关电压矢量,使电机能按控制要求调解输出转矩,最终达到调速的目的。由于电机转速和磁链的计算对控制系统性能影响较大,为了获得满意的转矩计算,仿真研究是最有效的工具和手段。
本文利用MATLAB/Simulink仿真工具对PMSMDTC系统进行仿真,详细介绍了DTC系统中各控制单元的搭建,为PMSM交流伺服系统数字化控制的实现提供了理论基础。
1永磁同步电机的直接转矩控制
1.1永磁同步电机的数学模型
对PMSM做如下假设:
- 定子绕组三相对称,各相绕组轴线在空间上互差120电角度;
- 转子上没有阻尼绕组,永磁体没有阻尼作用;
- 忽略磁路饱和、磁滞和涡流影响,可用叠加原理进行分析;
- 反电势正弦,定子电流在气隙中只产生正弦分布磁势,忽略高次谐波。
得α-β坐标系下PMSM电压方程分别为
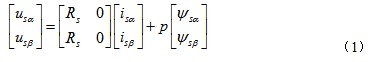
移向并积分得磁链方程为
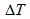
电磁转矩方程为
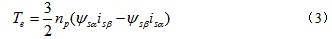
电力拖动系统运动方程
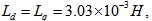
式中: 为定子磁链α、β轴分量;
为定子磁链α、β轴分量;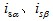 为定子电流α、β轴分量;
为定子电流α、β轴分量;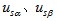 为定子电压轴分量;
为定子电压轴分量;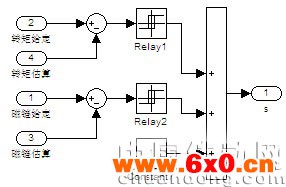 为定子绕组电阻;p为微分算子;
为定子绕组电阻;p为微分算子;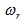 为转子机械角速度;
为转子机械角速度;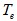 为电磁转矩;
为电磁转矩; 为电机极对数;
为电机极对数;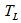 为负载转矩;J为电机转动惯量;B为粘滞系数。
为负载转矩;J为电机转动惯量;B为粘滞系数。
1.2直接转矩控制系统
DTC系统原理框图如图1所示,它由电压源逆变器、PMSM、电压计算、采样电流3s/2s、磁链估算、转矩估算、转子位置估算、PI调节器、滞环比较器、开关表等模块组成。
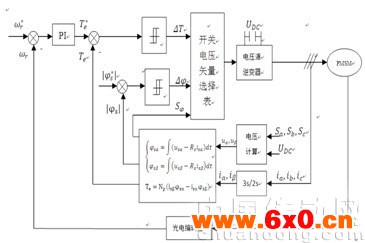
图1 直接转矩控制系统框图
1.3 电压矢量
三相电压型逆变器及电动机连接原理结构简图如图2所示,直流母线电压为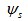 。六个开关管分别用理想开关1~6组成a、b、c三个桥臂,每个桥臂上下开关管互锁导通,分别用开关变量
。六个开关管分别用理想开关1~6组成a、b、c三个桥臂,每个桥臂上下开关管互锁导通,分别用开关变量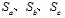 来表示a、b、c三个桥臂开关管开关情况。
来表示a、b、c三个桥臂开关管开关情况。
相应的逆变器输出电压空间矢量可表示为
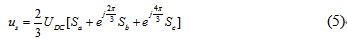
假设六个开关管作这样一个周期循环:456、561、612、123、234、345,则逆变器三相共有8种状态组合,其中6个非零电压矢量 、
、 、
、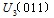 、
、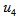 、
、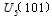 、
、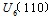 和两个零电压矢量
和两个零电压矢量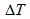 、
、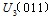 分布如图3所示。从逆变器的正常工作来看,前六种是有效的,后2种状态是无效的,因为这时逆变器并没有电压输出。
分布如图3所示。从逆变器的正常工作来看,前六种是有效的,后2种状态是无效的,因为这时逆变器并没有电压输出。
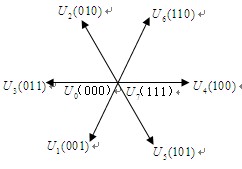
图2 三相电压型逆变器结构简图 图3 输出的空间电压矢量
2 系统的Simulink仿真组建
本仿真系统主要包括速度环PI调节器、采样电流3/2变换、定子磁链估算(包含电压计算)、转矩估算、区段判断、开关表的合理选择、开关矢量输出的定义等子模块组成。
2.1 坐标变换
在实际的直接转矩控制系统中,能采样到的电流是电机的三相电流,需要通过坐标变换才能得到需要的两相静止坐标系下的两相电流以便于计算,这就需要用到3/2变换。
坐标变换公式如下:
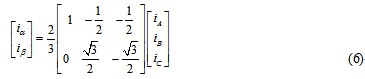
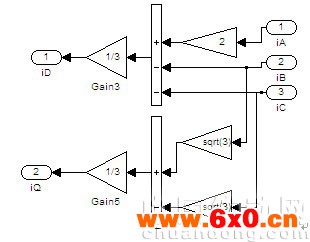
图4 采样电流的3/2变换
2.2 定子磁链和转矩估算模型
PMSM定子三相电压由式(7)计算:
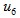
其中 是开关状态矩阵。
是开关状态矩阵。
由式(2)、(3)和(7)可组建定子磁链和转矩估算模型如图5和图6。
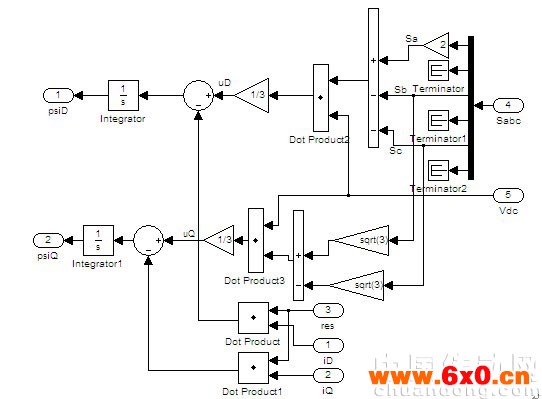
图5 定子磁链估算模型
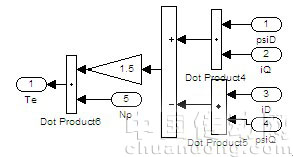
图6 转矩估算模型
2.3磁链幅值与角度计算模型
由公式(8)和(9)可得磁链幅值和角度计算模型如图7和图8所示。



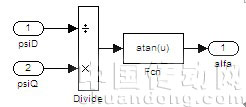
图7 磁链幅值计算模型 图8 转矩计算模型
2.4 区段判断模型
对照图3,做以下分区如表1所示,定子磁链矢量所在区段可以根据磁链在α-β坐标上的分量进行判定,由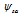 的正负确定定子磁链矢量的象限,再由式(9)决定定子磁链矢量的具体位置,实现模块如图9所示。
的正负确定定子磁链矢量的象限,再由式(9)决定定子磁链矢量的具体位置,实现模块如图9所示。
表1 磁链区段和角度的关系

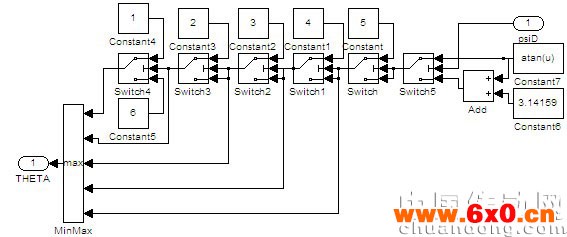
图9 区段判定模型
2.5 转矩磁链误差信号模型
在转矩控制系统中,转矩给定由给定转速通过PI调节器输出获得的,磁链和转矩的误差信号通过滞环比较器与反馈回来的区段值一起送给开关矢量表,通过查表的形式输出所需要的电压矢量。

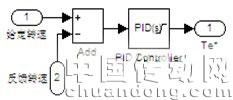
图10 转矩、磁链误差信号模型 图11 速度环PI调节器
2.6 开关表选择模型及其他模型
在直接转矩控制系统中,当施加电压矢量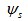 夹角大于
夹角大于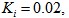 时,磁链幅值减小;当施加电压矢量
时,磁链幅值减小;当施加电压矢量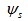 夹角小于
夹角小于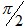 时,磁链幅值增加。当电压矢量落后于
时,磁链幅值增加。当电压矢量落后于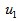 时,转矩减小;当电压矢量超前于
时,转矩减小;当电压矢量超前于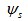 时,转矩增加。现用
时,转矩增加。现用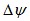 、
、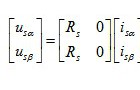 分别表示电机磁链和转矩的误差状态,当给定值比实际值大时状态为1,否则状态为0,则由
分别表示电机磁链和转矩的误差状态,当给定值比实际值大时状态为1,否则状态为0,则由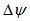 、
、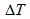 的状态以及反馈回来的区段值三者便可按表2进行开关电压矢量的选择。表2中的S是为了便于在Simulink中实现查表而设置的一个变量,其中
的状态以及反馈回来的区段值三者便可按表2进行开关电压矢量的选择。表2中的S是为了便于在Simulink中实现查表而设置的一个变量,其中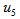 。
。
表2 DTC系统开关表


图12 开关选择表、逆变器及电机模型
其中Lookup Table(2-D)参数设置分别为:
Row index input values: int16([1,2,3,4]); Column index input values: uint16([1,2,3,4,5,6]);
Table data: uint16(reshape([1,2,5,6,5,3,4,2,4,1,6,3,6,5,2,1,2,4,3,5,3,6,1,4],4,6));
Embedded MATLAB Function中定义电压开关矢量M语言为:
function y = fcn(u)
y = [ 0; 0; 0; 0; 0; 0];
switch u
case 1
y= [ 0; 1; 0; 1; 1; 0]; %对应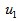 电压矢量
电压矢量
case 2
y= [ 0; 1; 1; 0; 0; 1]; %对应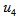 电压矢量
电压矢量
case 3
y= [ 0; 1; 1; 0; 1; 0]; %对应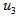 电压矢量
电压矢量
case 4
y= [ 1; 0; 0; 1; 0; 1]; %对应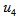 电压矢量
电压矢量
case 5
y= [ 1; 0; 0; 1; 1; 0]; %对应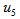 电压矢量
电压矢量
case 6
y= [ 1; 0; 1; 0; 0; 1]; %对应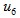 电压矢量
电压矢量
end
3 仿真结果及分析
本系统参数设定为:采样时间为10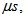 直线母线电压为310V,死区时间为2ms,限幅值为[-3,+3],
直线母线电压为310V,死区时间为2ms,限幅值为[-3,+3],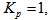
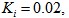 电机极对数
电机极对数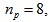 定子电阻
定子电阻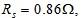 给定磁链
给定磁链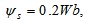 转动惯量
转动惯量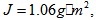 粘滞系数
粘滞系数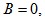 直、交轴的等效电感
直、交轴的等效电感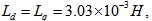 给定转速为50rad/s,在t=0s时刻电机空载启动,在t=0.2s时将给定转速突加到60rad/s,在t=0.3s突加0.7Nm的负载转矩,仿真时间为0.4s。电动机转速、定子磁链矢量、转矩、磁链的波形分别如图(a)、(b)、(c)、(d)。
给定转速为50rad/s,在t=0s时刻电机空载启动,在t=0.2s时将给定转速突加到60rad/s,在t=0.3s突加0.7Nm的负载转矩,仿真时间为0.4s。电动机转速、定子磁链矢量、转矩、磁链的波形分别如图(a)、(b)、(c)、(d)。


(a) 转速波形 (b) 定子磁链矢量波形
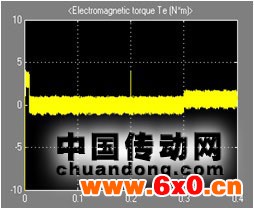

(c) 转矩波形 (d) 磁链波形
由仿真结果可以看出,电机启动速度很快,能快速跟踪给定转速;t=0.2s时给定转速由50rad/s突变为60rad/s,转速也能快速跟踪,转矩受到一定影响但很快就能够自动保持稳定;t=0.3s时突加负载,转速在允许范围内呈下降趋势但随后保持稳定,电磁转矩也很快稳定在设定值0.7Nm上下波动。
4 结论
在PMSM DTC理论的基础上,利用MATLAB/Simulink建立了PMSM DTC系统,仿真结果表明:波形符合理论分析,系统具有较好的静、动态特性。在建立实际系统前,通过仿真研究可以减轻大量的人力物力,尤其为PMSM DTC的软硬件设计提供了理论基础。
参考文献
[1] 刘英培,万健如,梁鹏飞. 基于扩展卡尔曼滤波器和空间电压矢量调制的永磁同步电机直接转矩控制[J]. 中国电机工程学报, 2009,29(27):67-74.
[2] Zhong L,Rahman M.F. Analysis of Direct Torque Control in Permanent Magnet Drives [J]. IEEE Transactions on Power Electronics,1997,12(3):528-535.
[3] 田淳,胡育文. 永磁同步电机直接转矩控制系统理论及控制方案的研究[J]. 电工技术学报,2002,(2):8-11.
[4] 杨建飞,胡育文. 永磁同步电机直接转矩控制转矩调节器设计[J]. 中国电机工程学报,2011,31(9):76-81.
[5] 童克文,张兴,张昱等. 基于新型趋近律的永磁同步电动机滑模变结构控制[J]. 中国电机工程学报, 2008,28(21):102-106.
[6] 周扬忠,胡育文. 交流电动机直接转矩控制[M]. 北京:机械工业出版社,2009,10.
[7] 谢运祥,卢柱强. 基于MATLAB/Simulink的永磁同步电机直接转矩控制仿真建模[J]. 华南理工大学学报,2004,32(1):19-23.
[8] 王成元,夏加宽,杨俊友等. 电机现代控制技术[M]. 北京:机械工业出版社,2009,1.
[9] 周扬忠. 电励磁同步电动机直接转矩控制理论研究及实践[D]. 南京:南京航空航天大学,2006.










 QQ交流群
QQ交流群

